非線形勾配磁場を用いた磁場焦点法とその関連諸法の研究経緯
山田芳文(宇都宮大学名誉教授)
1. 磁場焦点法の研究経緯
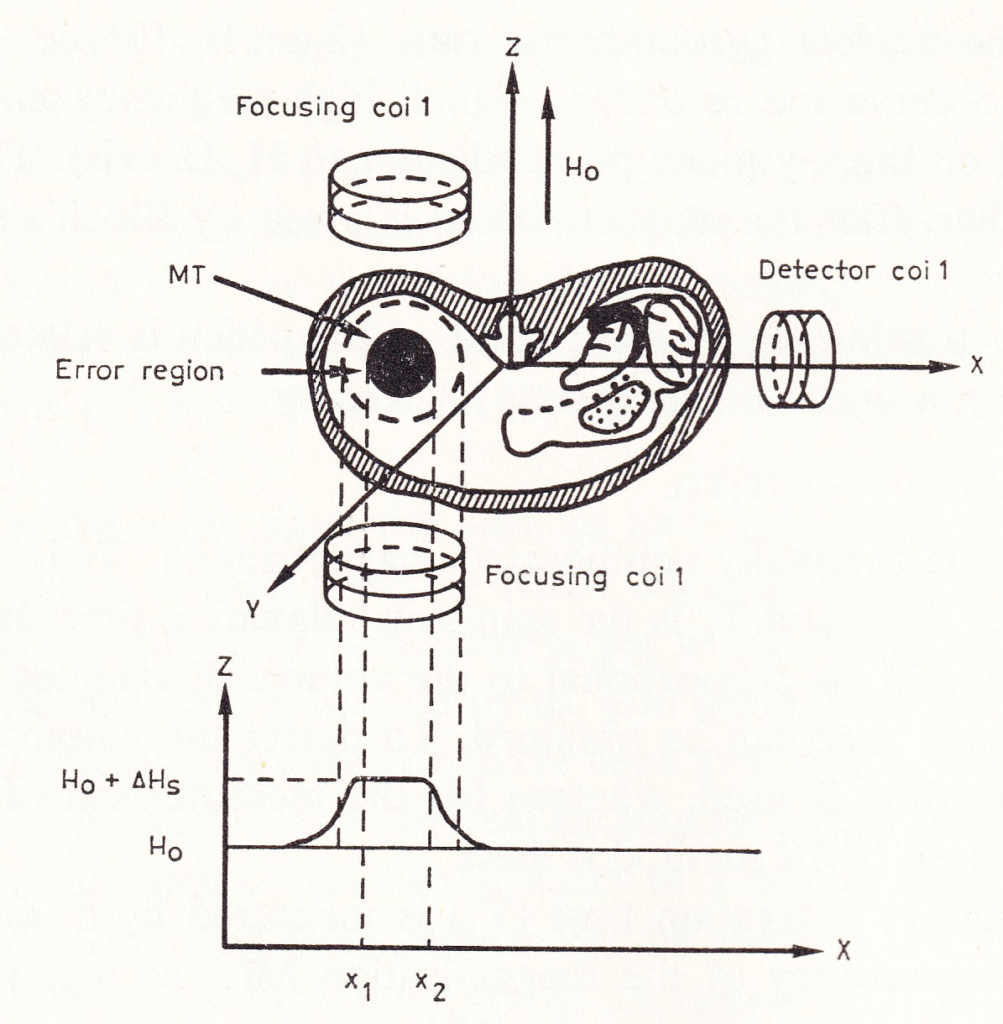
1970年代初頭に、NMRを生体情報の計測に応用しようという3つの研究が殆ど同時に、独立に発表された。表題に記された磁場焦点法は1972年に、北海道大学応用電気研究所に在籍された阿部善右衛門教授により提案された、非線形勾配磁場を用いてラーモア周波数の違いにより、生体内局所の情報を計測する我が国独自の方法[1][2]である。図1に磁場焦点法の原理図を示した[3]。
磁場焦点法の発表と前後して、Damadian氏によるFONAR(Field Focusing NMR)[4]、Lauterbur博士によるZeugmatography[5]の発表があり、Lauterbur博士の提案法はその後現在のMRIへと発展し、その功績によりLauterbur博士は2003年のノーベル医学・生理学賞を受賞している。一方Damadian氏のFONARは、技術的情報が明らかにされておらず、その詳細は不明である。
1974年からは山田も研究グループに参加した。磁場焦点法の実現に向けた焦点磁場の発生法、実験動物を用いたin vivo計測、計測部位に複数の緩和時間成分が存在する場合の、個々の緩和時間成分の分離法など、諸課題の検討[6]が阿部善右衛教授、田中邦雄博士、山田、ドクターコースの学生及び北海道大学医学部の先生を含めた研究グループで鋭意進められた。阿部善右衛門教授の定年退職後は、田中邦雄博士は旭川医科大学に、山田は宇都宮大学にとそれぞれ移籍したが、移籍後も互いに協力しあって研究を進めてきた。
磁場焦点法に於ける焦点磁場発生コイルシステムの例を図2、図3に示す。図2は、円形コイルの組み合わせによる焦点磁場発生コイルシステムの例である[7]。円型コイルペアによる半径方向の磁場強度変化と、軸方向の磁場強度変化の符号は逆になっており、中心と同じ強度の磁場等高面は半径方向と軸方行の中間方向に円錐状に延びたものとなる。このタイプの焦点磁場をその形状から星状焦点磁場と呼び、この焦点磁場を使用して担癌マウスの経時的T1変化モニタリングの検討が行なわれた[8]。
図3の平行四角柱コイルは、その各長辺に互いに逆向きの電流を与え、長軸方向を外部均一磁場の方向に向けて設置する[9]。外部均一磁場と平行四角柱コイルによる磁場のベクトル合成磁場の強度は、平行四角柱コイルの中心軸上で最小となり、軸から離れるに従い2次関数状に大きくなる。その磁場等高面は中心軸の回りに閉じた円筒形をなすものとなり、このタイプの焦点磁場をその形状から棒状焦点磁場と呼んだ。
図2、図3のコイルシステムで発生される焦点磁場は、両方とも磁場強度変化プロフィールを変えることなく、その中心位置を電気的に移動させる(空間的に走査する)ことが可能であり、イメージングにも応用することが出来る[9][10]。なお、図の簡略化のため、焦点磁場の空間的走査コイルについては、図2ではz方向の、また図3ではⅹ方向の走査コイルのみ示してある。
図4には、星状焦点磁場のポイント走査によって得られたシシトウの画像の例[10]を、図5には、棒状焦点磁場のライン走査によって得られた画像の例[9]を示す。
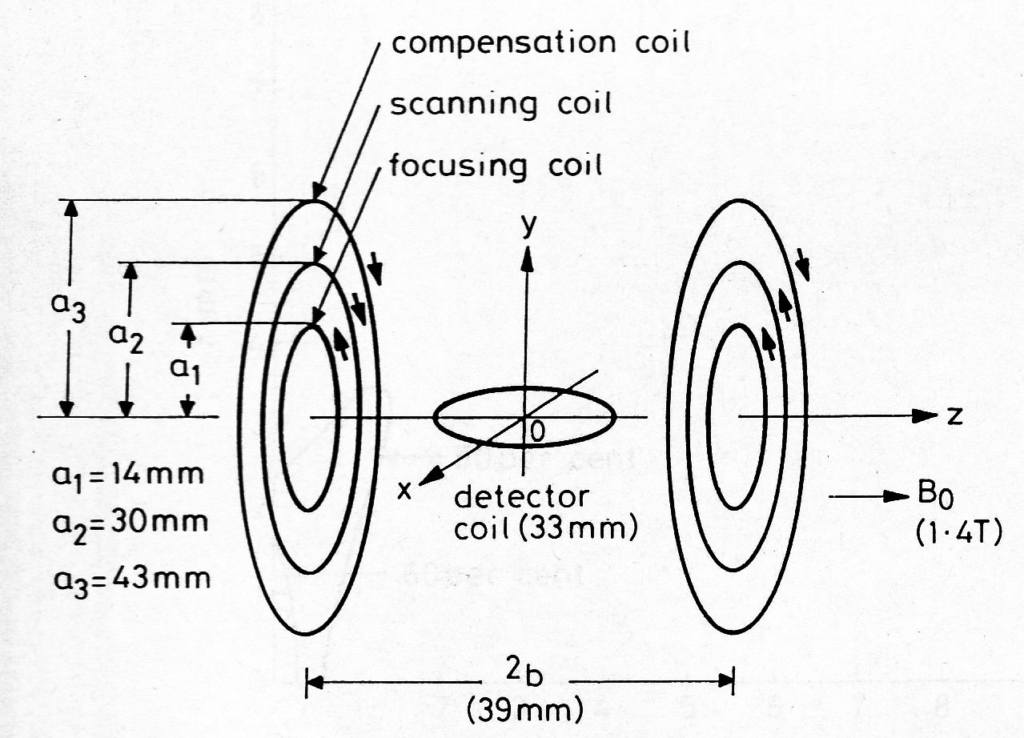
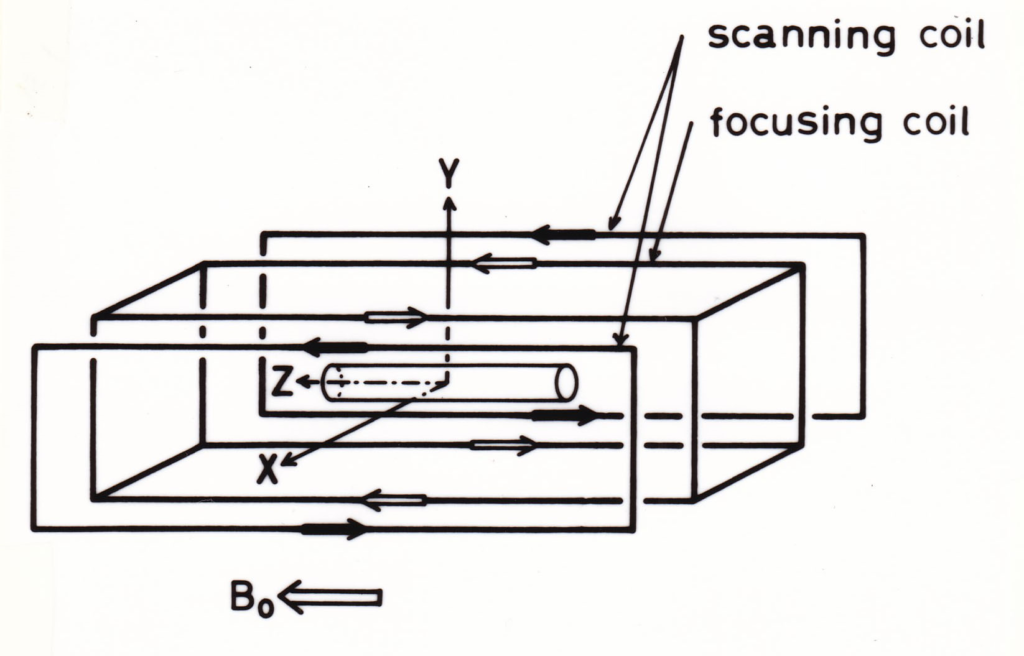
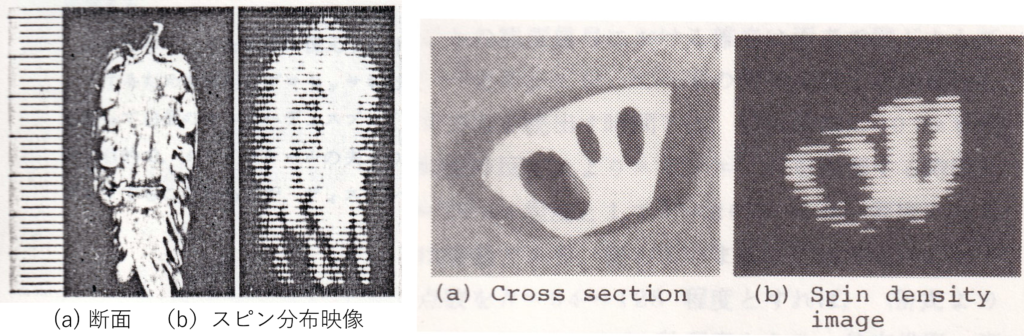
図6に山田が宇都宮大学に赴任してから試作した0.019テスラ棒状焦点磁場NMR映像装置を示す。静磁場発生ソレノイドコイルの中に四角柱形棒状焦点磁場発生コイル、同焦点磁場のx方向(図の左右方向)、y方向(上下方向)への走査用平行四辺形コイルが見える。四角柱形コイルの中心に直径6 cmのプローブコイルが置かれ、その静磁場方向(z方向)の両側にGzグラジエントコイルが置かれている。強い2次関数勾配磁場を発生させるのに四角柱コイルには大きなアンペア回数が必要とされるため、図のコイルシステムは物々しい形状をしている。後述のフレネル変換映像法の特徴磁場は、このコイルシステムに小さな電流を供給することにより、発生させている。なお、平行四角柱コイルの静磁場に直交する辺の電流は、特徴磁場の強度変化プロフィールに少なからぬ影響を及ぼすが、特徴磁場パルスの途中で励磁電流の極性を反転させることで簡単に補償することができる[11]。

磁場焦点法は、生体内部局所の情報を計測する方法であるので、映像法として利用することが出来ないことはないが、現在のMRIに比べて単位時間当たりのデータ収集量が少ないため、効率が非常に悪い。MRIでは、磁場を級数展開したときの1次項である線形勾配磁場が使われるのに対し、磁場焦点法の焦点磁場には、2次項の非線形勾配磁場が使用される。一般に、2次項の係数は1次項の係数よりかなり小さいため、人体程度の大きさの被写体に対して、局所測定領域を数mm以下に絞る強い非線形勾配磁場を用いた磁場焦点法MRIは、焦点磁場発生の難しさ、良好なS/Nの映像を得るためのデータ収集時間が、極めて長くなるなどの難点から、その実現は困難であるものと思われる。それに対して、測定NMR信号に被写体の広い領域からの寄与がある弱い2次関数勾配磁場を用いた映像法が、もし実現できるのであれば、その技術的難しさは通常の線形勾配磁場を用いるMRIと同程度であろうと考えられる。このような考察過程を経て考え出された方法が、フレネル変換映像法[12][13]である。
2. フレネル変換映像法とそれに関連する諸法の研究経緯
図3のコイルシステムに、小さい駆動電流を与えて発生される弱い2次関数勾配磁場(特徴磁場と呼ぶ)を、その中心位置を走査しながら収集したNMR信号は、光、電磁波などのフレネル回折場と同形の、更に簡単化された式で表されるものとなっている[12]。これは被写体スピン分布のフレネル変換に相当するものであり、スピン分布像は、電波映像レーダー (合成開口レーダー[14]) の場合と同様に、計算機処理により、再構成することができる。 図7は、0.019テスラ試作NMR装置で、フレネル変換映像法により得られたレンコンの映像例である。

物体光の波面情報を記録し、コヒーレント光で波面再生する技術がホログラフィであり、光学的なフーリエ変換、フレネル変換で映像再生を行う各種ホログラフィが知られている。
汎用MRI、位相拡散フーリエ法[15]、フレネル変換映像法の信号に、その値が負にならないよう正の定数項を重畳したものは、ホログラムに相当するものとなっていて光学的演算により、スピン分布像を再構成することが出来る(NMRホログラフィ)[16][17][18]。
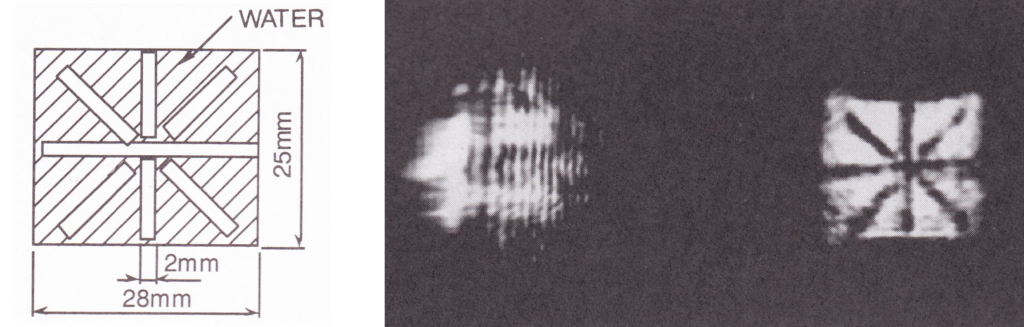
図8、図9にNMRフレネルホログラフィの実験に使われたファントーム形状と、そのNMRフレネルホログラムからの光学再生像の例を示す[16]。図9の右側の像が実像であり、左側の像は虚像である。
コンピュータの演算速度がそれ程速くなかった頃は、文字通り瞬時に映像再構成が行われる光学的方法は、インターベンショナルMRIへの応用の可能性があるため、幾つかの研究が行われた[19][20][21]。
フレネル変換映像法の映像再構成法には、収集データに2次関数の位相項を乗じた後、フーリエ変換する方法(方法1)と、コンボリューション積分を解く方法(方法2)の2つがある。(方法1)による再構成像のFOVは、2次関数特徴磁場の係数と特徴磁場パルス幅の積で決まるフレネル変換法パラメータに依存して変化するのに対し、(方法2)による再構成像のFOVは、フレネル変換法パラメータには無関係で、特徴磁場の走査幅に等しいという性質がある。また、フーリエ変換、フレネル変換は完全に可逆な演算であるので、信号をハードウェア的に装置から得ることもできるし、ソフトウェア的に画像から計算処理により得ることもできる。フレネル変換法の(方法1)、(方法2) 再構成法でFOVが異なる点に着目し、パラメータを適切に設定してMR画像から(方法2)で信号を作成し、次いで(方法1)で映像再構成を行うと、ウェーブレット解析で得られるような一種の多重解像度解析像が得られる。この領域でウィナーフィルタを掛けて雑音を除去した後、逆過程を辿って映像に戻ると、大幅にS/Nを改善したMR映像を得ることができる[22]。この方法は、FREBAS (FREsnel BAnd Sprit) 法と呼ばれたが[22]、医用画像で問題となる画像情報の損失が少なく、なおかつ雑音の除去効果が大きいという、特色ある雑音除去法である。
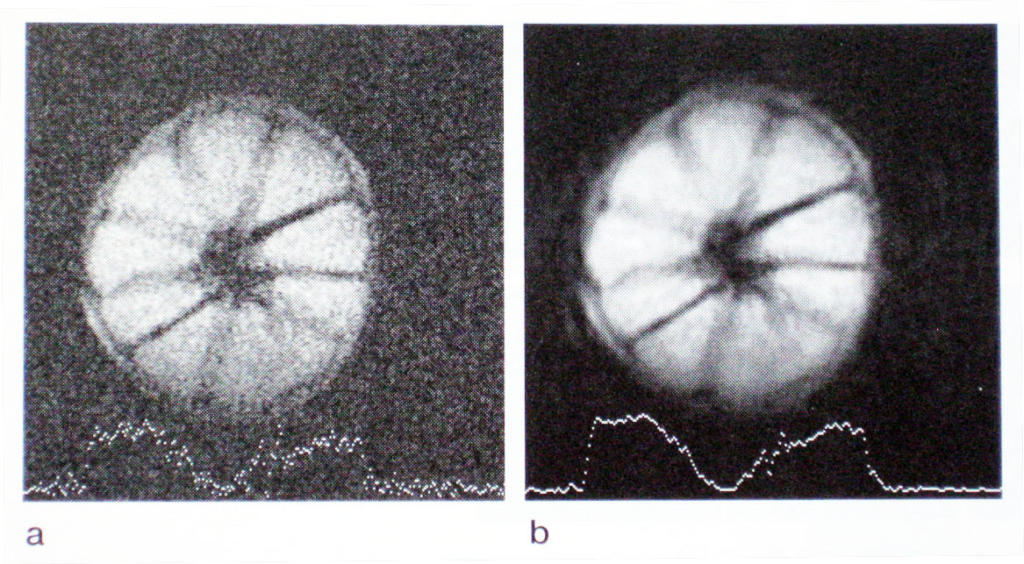
図10には、0.019テスラ試作MRI装置で撮像したポンカンの映像に、FREBAS法を適用した結果例を示す。
本文では、現在、臨床用に幅広く使われているMRIの黎明期に、MRIとは独立に提案された生体内部局所情報を計測する磁場焦点法と、その後2000年初頭頃までの研究発展の経緯について、その概要を述べた。
[文献]
[1] 阿部他;電子通信学会(現電子情報通信学会)技術報告, MBE72-20 (1972).
[2] 阿部他:日本国特許 No.13508 (1973)., アメリカ合衆国特許 No.3932805 (1976).
[3] K.Tanaka et al.:Biotelemetry, 4, 181 (1977).
[4] R. Damadian:Science, 171, 1151 (1971).
[5] P. C. Lauterbur:Nature,242, 190 (1973).
[6] Z.Abe et al.;Radiation Medicine, 2, No.1, 1 (1984).
[7] K.Tanaka et al.:Med. & Biol. Eng. & Comput., 30, 427 (1992).
[8] K.Tanaka et al.:Med. & Biol. Eng. & Comput., 33, 38 (1995).
[9] 山田他:電子情報通信学会論文誌, J70-C, No.3,416 (1987).
[10] 田中他:NMR医学 ― 基礎と臨床 ― , 核磁気共鳴研究会編(初版),110 , 丸善 (1984).
[11] 神崎他:電子情報通信学会論文誌, J81-D-II, No.12, 2867 (1998).
[12] 山田他:電子情報通信学会論文誌, J70-C, No.3, 439 (1987).
[13] Y. Yamada et al.:Rev. Sci. Instrum., 63, No.11, 5348 (1992).
[14] 安藤繁:計測と制御, 22, 209 (1983).
[15] A.A. Maudsley:J. Magn. Reson., 76, 287 (1988).
[16] 伊藤他:医用電子と生体工学, 34, No.3, 30 (1996).
[17] 伊藤他:電子情報通信学会論文誌, J84-D-II, No.2, 400 (2001).
[18] S. Ito et al.:IEEE Trans. Biomed. Eng., 49, No.6, 574 (2002)
[19] 伊藤他:電子情報通信学会論文誌, J81-D-II, No.1, 184 (1998).
[20] 伊藤他:日磁医誌, 22, No.3, 126 (2002).
[21] S. Ito et al.:Applied Optics, 41, No.26, 5527 (2002).
[22] 伊藤他:Med. Img. Technol., 19, No.5, 355 (2001).